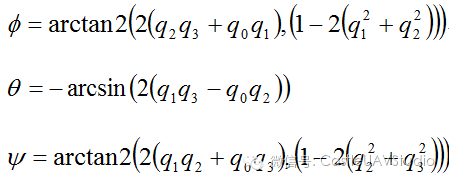请大家注意，此时，纵然出现90°的姿态角，由于没有出现分母为零的情况，因此依然有解。这只是很直观的验证，结合指数姿态表示方法：

　　而四元数的不唯一性可以通过下式看出：

　　因此，带入

　　时，R矩阵式一样的。

　　很容易获得从四元数到欧拉角的转换公式：

　　5)程序实现

　　从欧拉角到四元数的程序实现非常直接，并不需要想一般算法那样进行离散化，因为这里的转换公式并不对应时域函数，而是直接对应变量值，所以只要我们通过传感器获得可靠的姿态数据值后就可以直接带入公式求得对应姿态：

　　quat[0] = chphi0 * chtheta0 * chpsi0 + shphi0 * shtheta0 * shpsi0; quat[1] = -chphi0 * shtheta0 * shpsi0 + shphi0 * chtheta0 * chpsi0; quat[2] = chphi0 * shtheta0 * chpsi0 + shphi0 * chtheta0 * shpsi0; quat[3] = chphi0 * chtheta0 * shpsi0 - shphi0 * shtheta0 * chpsi0;

　　如是而已。

　　6）指数表现形式

　　指数表现形式在实际使用中比较少，但是对于理解另外两种旋转表现方式很有助益。它是既不是全局的，也具有奇异性。有兴趣的朋友可自行了解，推荐《A Mathematical Introduction to Robotic Manipulation》这本书。

　　相信大家通过本文应该可以直接获取无人机姿态数据的转换公式，并根据不同旋转运动描述方法的特点结合自己的需求进行数据转换（基坐标变换？不知这样的词汇合适么）。

　　有时我们面对的研究对象是可以碰触的物理数实体，比如无人机，这当然会给我们带来很多好处，但过分陷入到直观感受的依赖中，很有可能将自己引入主观的误区，就像一场狩猎游戏，好狐狸总是想方设法用猎人自己的思维来迷惑他。而数学却能简洁，工整，清晰的将我们研究对象的本质揭露出来，很多情况下这是我们凭自己的直观感受难以挖掘的，这也正如好的侦探，最后得出的结论也许很难在感情上接受它，却无法否认它是更加接近真相的推断。在无人机研究中畅快的运用数学就犹如身临一场狩猎或者探案冒险，抽丝剥茧，能得到一点点结论都会让自己心情久久畅快，有时会让自己惊讶的一天都沉迷其中，这种快乐也可以算作研究无人机的副产品吧：）。

　　有很多朋友私信或者值乎询问无人机行业中的职业选择与发展规划等方面的内容，MR.城堡计划在第二次Live中进行相关分享，欢迎有兴趣的朋友一起来探讨这个话题。

　　以往的文章及知乎Live可以从目录中查找

　　城堡无人机工作室微信公众号：CastleUAVStudio

　　文中图片来自于互联网